(something like that: 5,1,1,1,1,1 or 6,6,5,4,3,3,3,3,2,1,0,0,0 ) |
GREEN colour of the solution window = the given degree sequence IS graphic. RED = IS NOT graphic.
WHITE = It could not be determined due to an error in the given sequence (possibly
the input field box is empty or there is a comma after the last number, ...).
The calculation is based on the Havel-Hakimi algorithm.
WHITE = It could not be determined due to an error in the given sequence (possibly
the input field box is empty or there is a comma after the last number, ...).
The calculation is based on the Havel-Hakimi algorithm.
A graph (or a simple graph) G = (V, E) is a pair of sets (V, E) where:
V = {v1,v2, . . . ,vn} is a nonempty list called the list of vertices of G,
and E = {e1,e2, . . . ,en} is a list of edges e = {vi,vj} (unordered pairs of distinct elements of V).
The degree degG(v) of a vertex vi in an undirected graph G
is the number of edges e that are incident on the vertex vi.
The degree sequence D = {d1,d2, . . . ,dn} is a list of sorted nonnegative integer numbers.
If we have a nonincreasing, finite degree sequence of nonnegative integers,
we can test whether this degree sequence is graphic by applying the Havel-Hakimi algorithm.
So the question is: Is there a graph G with n - vertices,
where degree sequence di = degG(vi), for every i = 1,2,...,n ?
V = {v1,v2, . . . ,vn} is a nonempty list called the list of vertices of G,
and E = {e1,e2, . . . ,en} is a list of edges e = {vi,vj} (unordered pairs of distinct elements of V).
The degree degG(v) of a vertex vi in an undirected graph G
is the number of edges e that are incident on the vertex vi.
The degree sequence D = {d1,d2, . . . ,dn} is a list of sorted nonnegative integer numbers.
If we have a nonincreasing, finite degree sequence of nonnegative integers,
we can test whether this degree sequence is graphic by applying the Havel-Hakimi algorithm.
So the question is: Is there a graph G with n - vertices,
where degree sequence di = degG(vi), for every i = 1,2,...,n ?
degG(v) - degree of vertex v is the number of edges e ∈ E that are incident on the vertex v ∈ V
δ(G) - the smallest degree of the graph G
Δ(G) - the largest degree of the graph G
nonempty - containing at least one element
δ(G) - the smallest degree of the graph G
Δ(G) - the largest degree of the graph G
nonempty - containing at least one element
It is possible for two topologically distinct graphs to have the same degree sequence.
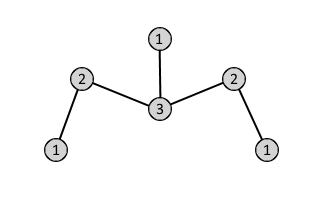
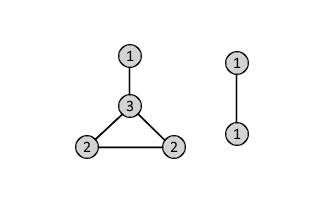


The example above shows two (isomorphic) graphs that have the same degree sequence = (3,2,2,1,1,1)
There are examples of degree sequences that are graphic:
D = (4,2,2,2,2)
D = (5,1,1,1,1,1)
D = (6,6,5,4,3,3,3,3,2,1,0,0,0)
And few examples of degree sequences that are not graphic:
D = (1,1,1)
D = (4,2,2,2)
D = (4,2,2,2,2)
D = (5,1,1,1,1,1)
D = (6,6,5,4,3,3,3,3,2,1,0,0,0)
And few examples of degree sequences that are not graphic:
D = (1,1,1)
D = (4,2,2,2)